An experiment is done using a special chemical that includes methylene blue, a compound that turns blue in the presence of oxygen. Three test tubes containing various plant cells exposed to different levels of light are observed over 3 days. Each day the test tube was placed in a photospectrometer and the light transmittance were recorded in the following table.
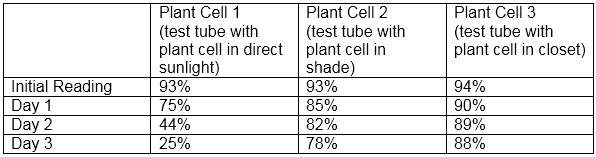
Which of the following is a possible explanation for the percent transmittance reported for Plant Cell 2?

Loading ...
Correct Answer: D. The plant went through photosynthesis but at a lower rate than normal.
The plant cell in shade has some access to sunlight, but it is limited since the cell is in the shade. Since methylene blue is in the test tube, the color in the test tube should become darker, more and more blue as the plant produces oxygen and goes through photosynthesis. Plant cell 1 is the control group and as you can see the percent transmittance of light decreases over the 3 days because of the high rate of photosynthesis and production of oxygen. The plant cell in the closet had no access to sunlight and was able to go through some photosynthesis on the first day but virtually none the other 2 days, which is why the percent transmittance remained high, signaling low levels of oxygen produced and low levels of blue pigment present.
Get it right? Tweet at us!
Subscribe below to get the DAT Question of the Day delivered straight to your inbox every morning.