A friend of yours draws a circle circumscribing a regular octagon. What is the ratio of the area of the octagon to the circle?

Loading ...
Correct Answer: E. (2√2)/π
There are several ways you can compute the area of the octagon. No matter which way you choose, all of them will be easier if you draw the picture.
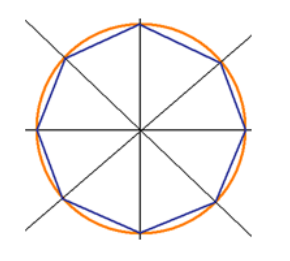
Notice how our octagon is made up of 8 isosceles triangles with leg length equal to that of the radius of the circle. Recall that the area of a triangle is 1/2 ABsin(c). In this case the angle
c is 45° as it is a regular octagon. The area of the octagon will be 8 * 1/2 r^2 sin(45°) = r^2 2√2. The area of a circle is simply πr^2. This means the ratio of the octagon to the circle is 2√2/π.
Get it right? Tweet at us!
Subscribe below to get the DAT Question of the Day delivered straight to your inbox every morning.